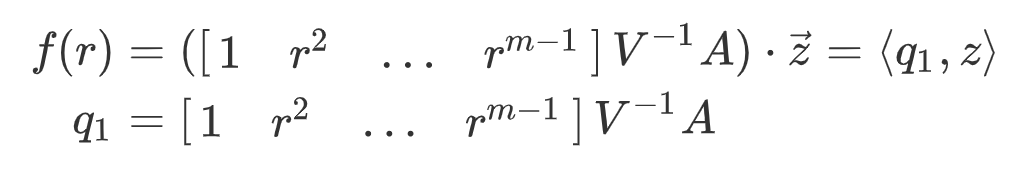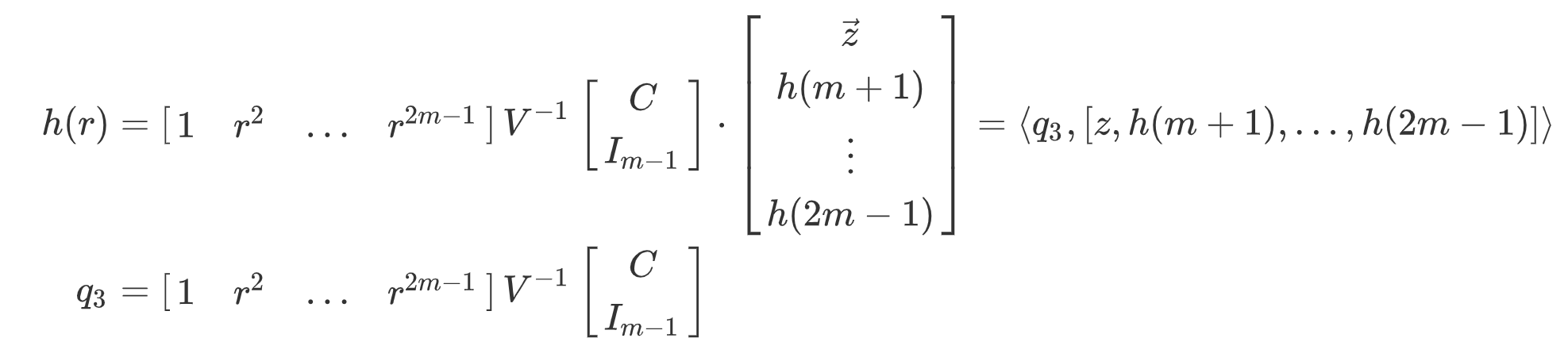Back
开发

从零知识证明到ETH智能合约

很好玩

零知识证明

什么是零知识证明

零知识证明指的是，证明者能够在不向验证者提供任何有用的信息的情况下，使验证者相信某个论断是正确的——存在一个双方已知的问题，我虽然知道答案，但不能透露答案是什么，同时证明我确实知道这个答案。

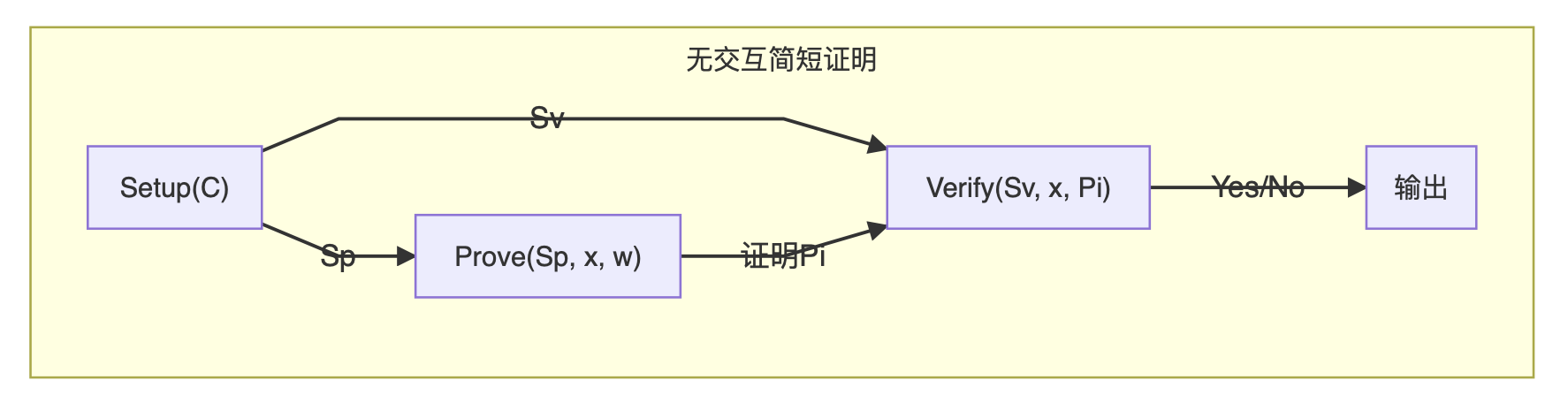
而当下应用最广泛的零知识证明被称为zk-SNARK(Zero-Knowledge Succinct Non-Interactive Argument of Knowledge)，即“零知识”、“简洁”、“非交互性”的“知识证明”，这几个要素可以通过模块化的方式逐步构建。

知识证明

简单的例子

阿里巴巴
阿里巴巴

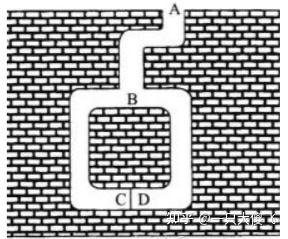
1.强盗在A点站立，并让阿里巴巴走到B点，阿里巴巴随机的从左右两个方向进入洞穴，因此阿里巴巴可能到达C处，也可能到达D处 2.强盗走到B点，并随机让阿里巴巴从左边或从右边出来。如果阿里巴巴拥有密门的咒语，那么无论他现在在C点或者是在D点都可以按照强盗的指令从正确的方向走出洞穴；但如果阿里巴巴如果没有密门的咒语，那么他只有$\frac{1}{2}$的可能从正确的方向出来

在这个场景下，通过k轮检查的概率为$(\frac{1}{2})^k$，只要通过足够多轮次的检查，就有极大的把握证明阿里巴巴拥有密门的咒语。

PCP定理

PCP，全称Probabilistically Checkable Proof，意思就是，所有的NP问题，都可以在多项式时间内通过概率验证的方法被证明。

因为所有的NP问题都可以有效地转换为数学运算电路，PCP定理指出，对于所有的电路$C$，我们都可以构造一套概率验证体系$(S, P, V)$，其工作方式如下：

$$ \forall C: \exists \text{ Proof System } (S, P, V): \\ S(C) \rightarrow (S_p, S_v) $$ S为生成算法Setup，把电路C转换成后续会用到的随机参数。

证明体系
证明体系

证明方通过公有和私密输入生成一个证明$\pi$，并且把证明$\pi$存入只读区域后共享给验证方查看（只读区域可以防止双方篡改证明内容）。唯一不同的是验证方并不能看到所有的$\pi$，只能通过一个query机制来检查这个证明$\pi$随机的$k$位数。通过看完这$k$位数之后，验证方就需要输出验证结果。

而把程序转换为数学运算电路这一过程，通常使用R1CS来完成

R1CS

R1CS，全名为Rank-1 Constraint System，具有如下形式： $$ \exists \vec{z} : (A \cdot \vec{z}) \circ (B \cdot \vec{z}) = C \cdot \vec{z} $$ $\vec{z}$表示程序的变量($x_i$)和输入($w_i$)，其中添加了作为常数使用的1 $$ \vec{z} = \begin{bmatrix}1\\x_i\\..\\w_i\end{bmatrix} $$ $\circ$表示逐项积，即 $$ A = \begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32}\end{bmatrix}, \ B = \begin{bmatrix}b_{11} & b_{12} \\ b_{21} & b_{22} \\ b_{31} & b_{32}\end{bmatrix}, \ C = A \circ B = \begin{bmatrix}a_{11} \cdot b_{11} & a_{12} \cdot b_{12} \\ a_{21} \cdot b_{21} & a_{22} \cdot b_{22} \\ a_{31} \cdot b_{31} & a_{32} \cdot b_{32}\end{bmatrix} $$ 通过R1CS，可以表达一种规则简单的一阶方程组，其中的方程形如$(2 \cdot x_1 + 5 \cdot x_2) \cdot (x_1 - 1) = 0$此类

任意的程序在“拍平”后都可以通过R1CS得到表达：

  1. x = y (y可以是变量或者数字)
  2. x = y op z (op 是二元运算符，可以是 +, - , *, /运算，y，z 可以是变量，数字或者子表达式)

例如

def qeval(x):
  y = x**3
  return x+y+5

可以拍平为

sym_1 = x * x
y = sym_1 * x
sym_2 = y + x
~out= sym_2 + 5
具体计算

我们假设要证明一下某个电路的私密输入$w$的值在0到15之间，由于R1CS仅能提供相等约束，所以这里的思想类似数电的构造逻辑电路，按位拆分判断 $$ 2^0 \cdot w_0 + 2^1 \cdot w_1 + 2^2 \cdot w_2 + 2^3 \cdot w_3 - w = 0 \\ w_0 \cdot (w_0 - 1) = 0 \\ w_1 \cdot (w_1 - 1) = 0 \\ w_2 \cdot (w_2 - 1) = 0 \\ w_3 \cdot (w_3 - 1) = 0 $$ $w_i$是$w$的按位拆分，而这里的输入$\vec{z}$即为 $$ \vec{z} = \begin{bmatrix} 1 \\ w \\ w_0 \\ w_1 \\ w_2 \\ w_3 \end{bmatrix} $$ 进而得到矩阵$A,B,C$ $$ A = \begin{bmatrix} 0 & -1 & 1 & 2 & 4 & 8 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix}, \ B = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \\ -1 & 0 & 1 & 0 & 0 & 0 \\ -1 & 0 & 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 0 & 1 & 0 \\ -1 & 0 & 0 & 0 & 0 & 1 \end{bmatrix}, \ C = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} $$ 这样，我们得到了一个最简单的$S(C)$，只要证明者将自己的“证明”$\vec{z}$传给验证者，验证者将其带入矩阵$A,B,C$检验方程的解，即可确认证明。当然，目前为止这个证明既不“零知识”（验证者可以在 $\vec{z}$中查看所有的私密输入$w$），也不高效（需要通过$O(n^{2.X})$的矩阵运算检验全部约束），需要一点点来完善。

简洁性

从PCP到LPCP

换一个实际一点的例子

假如A需要向B证明她拥有一个从0到100依次升序排列的数组，那么B可以通过随机抽查的方式来验证A的数组是否正确排列。

B可以抽查第49位是不是48，第3位是不是2等等来确定A是否真的拥有这么一个数组。当然，A也有可能是运气好，除了第49位和第3位其他都是乱序的。

不过当抽查的次数越来越多，A作假的可能性也会越来越低。

但是，这种单纯的抽查效率是非常低下的，验证的确信程度随着抽查次数线性提高，想要以接近100%的把握检验就需要抽查整个数组，不满足“简洁性”的需求，因此要增加额外的约束，线性PCP(Linear PCP/LPCP)。

如果说PCP形容的是所有NP范围内的问题都可以通过简短的随机抽验来验证，LPCP则是说任意一个$d$阶的多项式$P$，都可以通过随机验证多项式在几个点上取值来确定这个多项式的每一项系数是否满足特定的要求。

LCPC
LCPC

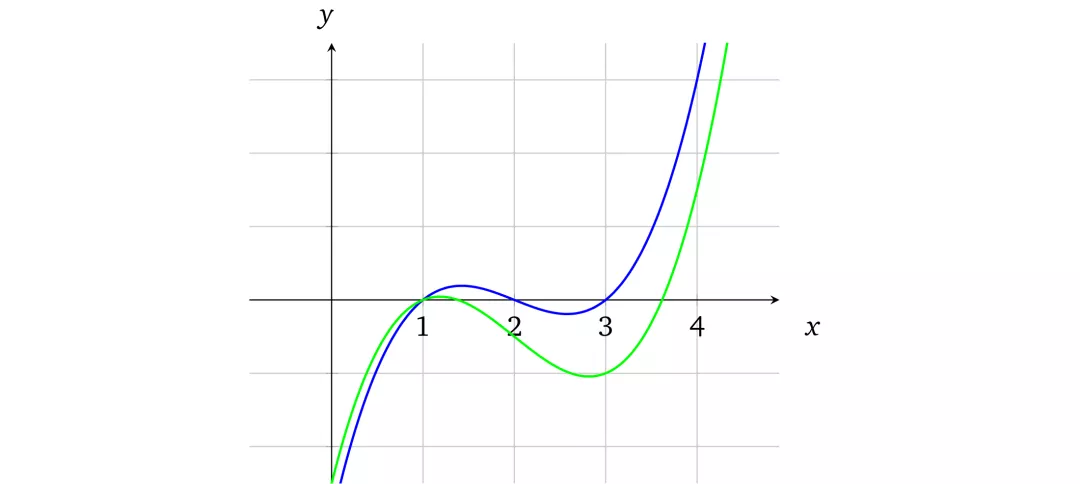
$f(x)=x^3–6x^2+11x–6$与$f(x)=x^3–6x^2+10x–5$相比，仅修改了一个系数，但两条曲线之间差别很大。根据代数基本定理，两个$d$阶的不同系数的多项式，在所有整数范围$F$内，最多也只会有$d$个点重合。所以，只要我们取出少量的点检验多项式的值是否符合预期，即可检验整个多项式是否满足要求，进而证明该多项式的全部系数均符合性质。这样，只要能够以某种方式把R1CS得到的$A \cdot \vec{z}, B \cdot \vec{z}, C \cdot \vec{z}$三个矩阵转换为多项式$P, Q, R$，就能通过计算多项式上某点的值快速地检验整个约束方程的正确性。（当然，谁来算，怎么防止作弊，还是一个问题）

从R1CS到QAP

从问题的本质考虑，转换后的多项式$P, Q, R$应当具有某种可检验的性质，其中最直观的性质应该形同R1CS，即$P \cdot Q = R$

而根据代数基本定理，只要我们采用插值的方式，构造满足$P(i) \cdot Q(i) = R(i), i \in [1, 2n]$的$n$阶$P$，$n$阶$Q$，$2n$阶$R$，就可以满足上面的性质

由于$P \cdot Q$为两个$n$阶多项式相乘，$R$应为$2n$阶多项式，需要使用$2n$个点进行插值。

至于额外的$n$个点，我们可以先通过$n$个点插值算出$P, Q$，再对$P \cdot Q$取点计算得到。

选取$[1, 2n]$是为了后续构建范德蒙矩阵便于求逆

首先以$A \cdot \vec{z}$为例，其计算结果是一个5x1的向量 $$ A \cdot \vec{z} = \begin{bmatrix} 0 & -1 & 1 & 2 & 4 & 8 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ w \\ w_0 \\ w_1 \\ w_2 \\ w_3 \end{bmatrix} = \begin{bmatrix} -w + w_0 + 2w_1 + 4w_2 + 8w_3 \\ w_0 \\ w_1 \\ w_2 \\ w_3 \end{bmatrix} $$ 可以构造$P$为 $$ \exists P(x) = f_0 + f_1 \cdot x + f_2 \cdot x^2 + f_3 \cdot x^3 + f_4 \cdot x^4 : \\ \begin{bmatrix} P(1) \\ P(2) \\ P(3) \\ P(4) \\ P(5) \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1^2 & 1^3 & 1^4 & 1^5 \\ 1 & 2 & 2^2 & 2^3 & 2^4 & 2^5 \\ 1 & 3 & 3^2 & 3^3 & 3^4 & 3^5 \\ 1 & 4 & 4^2 & 4^3 & 4^4 & 4^5 \\ 1 & 5 & 5^2 & 5^3 & 5^4 & 5^5 \end{bmatrix} \times \begin{bmatrix} f_0 \\ f_1 \\ f_2 \\ f_3 \\ f_4 \end{bmatrix} = \begin{bmatrix} -w + w_0 + 2w_1 + 4w_2 + 8w_3 \\ w_0 \\ w_1 \\ w_2 \\ w_3 \end{bmatrix} $$ 进而使用范德蒙逆矩阵计算多项式$P$的各项系数 $$ \begin{bmatrix} 1 & 1 & 1^2 & 1^3 & 1^4 & 1^5 \\ 1 & 2 & 2^2 & 2^3 & 2^4 & 2^5 \\ 1 & 3 & 3^2 & 3^3 & 3^4 & 3^5 \\ 1 & 4 & 4^2 & 4^3 & 4^4 & 4^5 \\ 1 & 5 & 5^2 & 5^3 & 5^4 & 5^5 \end{bmatrix}^{-1} \times \begin{bmatrix} -w + w_0 + 2w_1 + 4w_2 + 8w_3 \\ w_0 \\ w_1 \\ w_2 \\ w_3 \end{bmatrix} = \begin{bmatrix} f_0 \\ f_1 \\ f_2 \\ f_3 \\ f_4 \end{bmatrix} $$ 对$B \cdot \vec{z}$同理 $$ \exists Q(x) = g_0 + g_1 \cdot x + g_2 \cdot x^2 + g_3 \cdot x^3 + g_4 \cdot x^4 : \\ Q(1) = 1 \\ Q(2) = w_0 - 1 \\ Q(3) = w_1 - 1 \\ Q(4) = w_2 - 1 \\ Q(5) = w_3 - 1 \begin{bmatrix} 1 & 1 & 1^2 & 1^3 & 1^4 & 1^5 \\ 1 & 2 & 2^2 & 2^3 & 2^4 & 2^5 \\ 1 & 3 & 3^2 & 3^3 & 3^4 & 3^5 \\ 1 & 4 & 4^2 & 4^3 & 4^4 & 4^5 \\ 1 & 5 & 5^2 & 5^3 & 5^4 & 5^5 \end{bmatrix}^{-1} \times \begin{bmatrix} 1 \\ w_0 - 1 \\ w_1 - 1 \\ w_2 - 1 \\ w_3 - 1 \end{bmatrix} = \begin{bmatrix} g_0 \\ g_1 \\ g_2 \\ g_3 \\ g_4 \end{bmatrix} $$ 对$C \cdot \vec{z}$，如方才提到，需要额外取点$[n+1, 2n]$补充 $$ \exists R(x) = h_0 + h_1 \cdot x + h_2 \cdot x^2 + \dots + h_8 \cdot x^8 : \\ Q(1) = 0 \\ Q(2) = 0 \\ Q(3) = 0 \\ Q(4) = 0 \\ Q(5) = 0 \\ Q(6) = P(6) \cdot Q(6) \\ Q(7) = P(7) \cdot Q(7) \\ Q(8) = P(8) \cdot Q(8) \\ Q(9) = P(9) \cdot Q(9) \begin{bmatrix} 1 & 1 & 1^2 & 1^3 & 1^4 & 1^5 \\ 1 & 2 & 2^2 & 2^3 & 2^4 & 2^5 \\ 1 & 3 & 3^2 & 3^3 & 3^4 & 3^5 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 9 & 9^2 & 9^3 & 9^4 & 9^5 \end{bmatrix}^{-1} \times \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ P(6) \cdot Q(6) \\ P(7) \cdot Q(7) \\ P(8) \cdot Q(8) \\ P(9) \cdot Q(9) \end{bmatrix} = \begin{bmatrix} h_0 \\ h_1 \\ h_2 \\ \vdots \\ h_8 \end{bmatrix} $$ 至此就完成了矩阵$A, B, C$到多项式$P, Q, R$的转化，大大降低了检验的运算量。当然，范德蒙矩阵求逆需要$O(n^2)$，和直接检验R1CS在效率上没有什么本质区别，因此实际中会采用FFT等更高效的方式来求解合适的多项式，这里包括下文采取矩阵运算仅是便于理解算法流程。

从QAP到LPCP

hugo的latex支持过于拉胯

对于上面的QAP构造，我们可以优化一下计算的过程：

latex_1
latex_1

一旦转换成最后形态的表达式之后，我们马上可以发现，由于$V$与R1CS矩阵$A$是证明方和验证方都公开的内容，$r$是验证方选择的随机抽验的取值点，所以我们可以把整个表达式分成两个部分：

latex_2
latex_2

左边部分我们用一个向量$q$来表示，代表证明方想要验证的query。右边部分就是包含了证明电路中公有和私密输入的矩阵$z$。对于多项式$g$，我们也如法炮制，得到另一对内积组合$\langle q_2, z \rangle$。

最后对于多项式$h$，我们进行类似的操作。为了让整体的维度保持一致，我们需要额外加上一组单位矩阵：

latex_3
latex_3

当我们成功的把多项式随机取值问题分解为三个query向量$q1,q2,q3$之后，我们就可以正式地进入真正的LPCP验证协议了。

  1. 首先，证明方Prover事先计算好证明$\pi = [w, h(m+1), …, h(2m-1)]$，并且把证明保存起来，不许修改它。

    至于验证者如何确认证明$\pi$没有被修改，这点可以放到最后进行补充。

  2. 验证方Verifier随机的抽选一个验证点$r \stackrel{R}{\leftarrow} \mathbb{F}$，并且根据$r$取值计算得到三个query的向量$q_1,q_2,q_3$。

  3. 这三个Query需要和我们原本的输入向量$z = \begin{bmatrix}1\ x\ w \end{bmatrix}$相乘。我们观察这个向量之后发现，验证方事先已经可以得知向量的上半部分$\begin{bmatrix}1\ x\end{bmatrix}$。所以验证方可以把Query向量$q_i$进行切割，变成$[q_i^L, q_i^R]$两部分。这样的话，原本的计算也可以一分为二，然后把两部分的内积分别对叠起来：

$$ \langle q_i, z \rangle = \begin{bmatrix} \langle q_i^L, \begin{bmatrix}1\\x\end{bmatrix} \rangle\\ \langle q_i^R, \begin{bmatrix}w\end{bmatrix} \rangle\end{bmatrix} $$

  1. 通过这一步切割，我们发现对于$q_i^L$部分的计算，验证方已经全部知道了，所以我们可以进一步的优化证明方需要做的计算，只把$q_i^R$发送给证明方，让证明方仅仅与私密输入$w$相乘。
  2. 综上所述，验证方现在可以发送$q_1^R, q_2^R, q_3^R$三个query向量给证明方。
  3. 证明方收到query向量之后，只需要把每个值和自己的证明向量$\pi$相乘。

$$ a = \langle [q_1^R 0^{m-1}], \pi \rangle\\ b = \langle [q_2^R 0^{m-1}], \pi \rangle\\ c = \langle q_3^R, \pi \rangle $$

由于证明向量$\pi$后面还带了多项式$h$的额外$m−1$个取值点，所以我们需要在$q_1^R, q_2^R$的背后补上一个空白矩阵，才可以适配矩阵相乘的维度。

随后，证明方把$a,b,c$三个值发回给验证方。

  1. 最后，验证方只需要把左侧query的内积补上，最后检查等式是否相等：

$$ (\langle q_1^L, [1, x] \rangle + a) \cdot (\langle q_2^L, [1, x] \rangle + b) \stackrel{?}{=} (\langle q_3^L, [1, x] \rangle + c) $$

组合起来之后，这也就是变相检查等式$\langle q_1, z \rangle \cdot \langle q_2, z \rangle \stackrel{?}{=} \langle q_3, z \rangle$是否相等。

如果得到的$a,b,c$所组成的等式的确相等，那么就代表$h(r) = f(r) \cdot g(r)$。根据我们上文讨论的关系，这也就直接代表了$(A \cdot \vec{z}) \circ (B \cdot \vec{z}) = C \cdot \vec{z}$

Merkle Tree(题外话)

虽然这里用不到，但是merkle tree是一个匿名货币中非常常用的技术

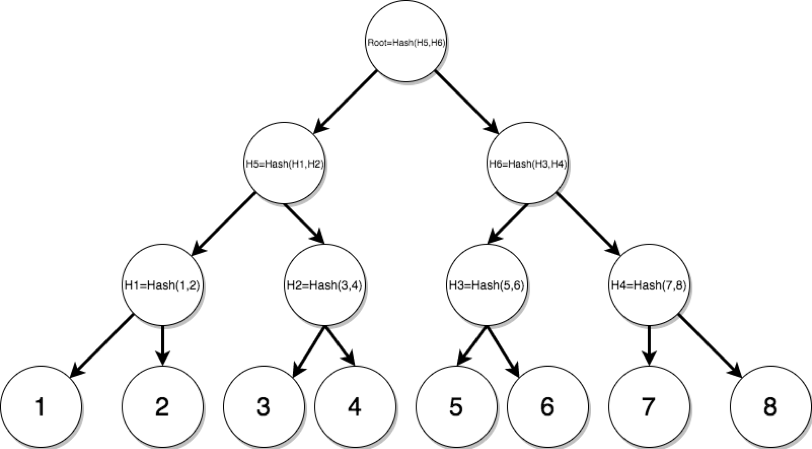
merkle tree
merkle tree

Merkle Tree是一种二叉哈希树，构建方式如上，常用于检验数据的完整性——其优势在于不需要下载完整的数据或者merkle tree，便可检验一个数据块是否属于整个数据。

Merkle证明

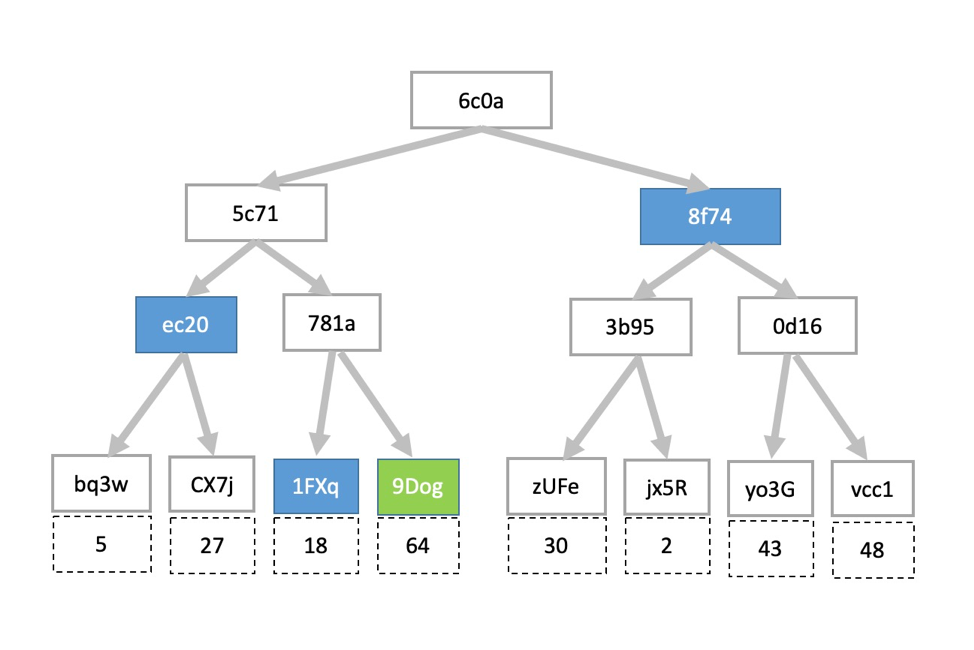
merkle proof
merkle proof

当需要证明数据64存在于整个数据块中时，仅需要传递merkle tree中每层的兄弟节点，即可自下向上计算出根节点6c0a。基于哈希的抗碰撞性，只要根节点6c0a对双方预先公开，攻击者就无法伪造其中的merkle路径。

非交互

Fiat-Shamir Heuristic(题外话)

这里同样用不上

Fiat-Shamir Heuristic是一个基于随机预言机假设的启发法，可以把任何交互式的随机验证协议(Public-coin Protocol)转换为非交互式的协议。

随机预言机，是一种理想机器，无论输入的是什么，输出的值我们都可以看作是一个和输入没有关联的随机数。这里用到的假设是哈希函数是随机预言机（未证明，但好用），当我们有了这个假设之后，我们就可以把交互式协议$I$压缩成非交互式协议$I'$了：

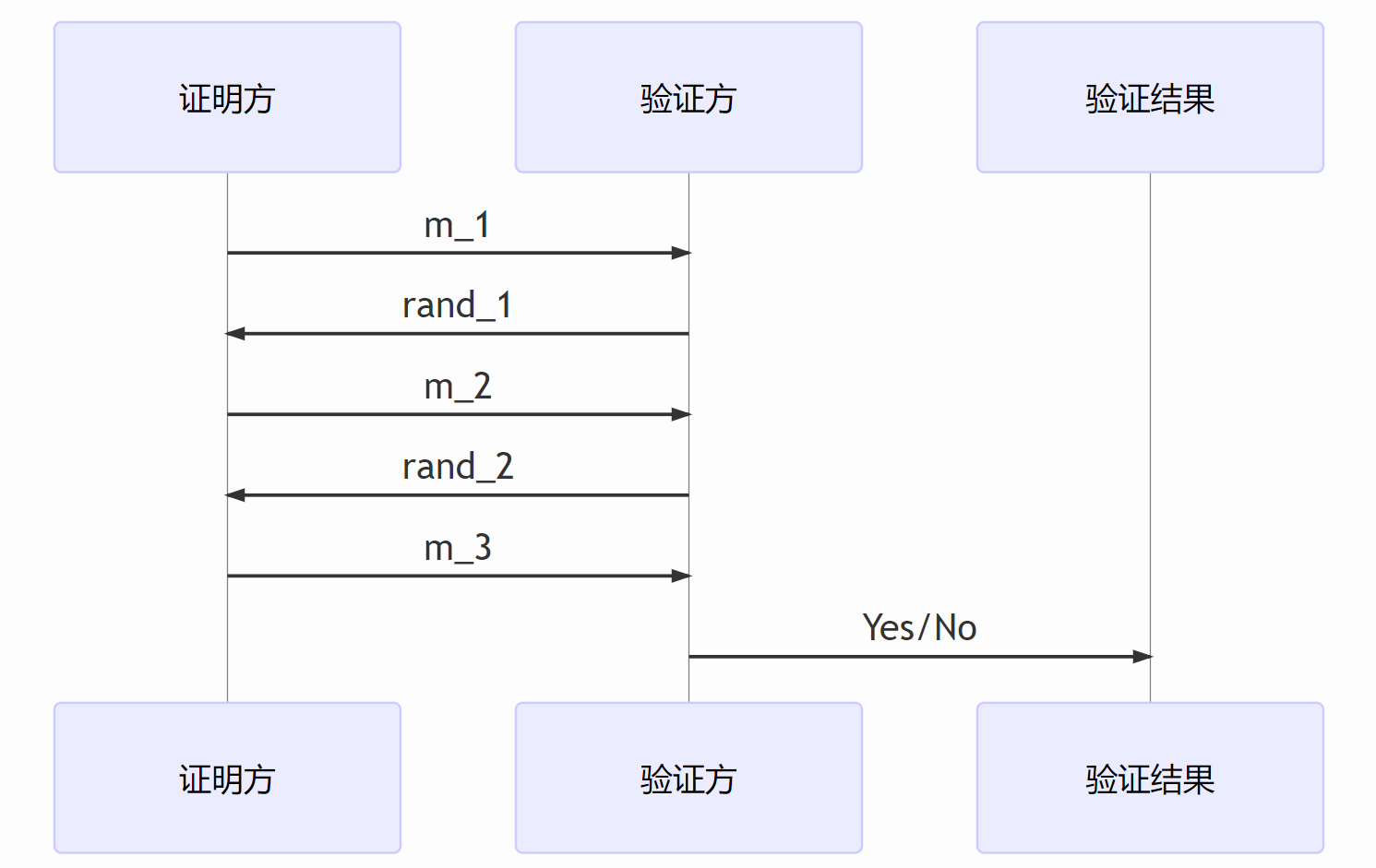
下面是一个假想的交互协议$I$

交换协议
交换协议

  1. 首先，证明方需要生成消息$m_1$。然后根据$m_2$的值来生成原本由验证方来生成的$rand_1 \leftarrow H(x, m_1)$。
  2. 随后，证明方根据$rand_1$的值来生成消息$m_2$，然后同理得到$rand_2 \leftarrow H(x, m_1, m_2)$。
  3. 最后，证明方生成$m_3$，并且把$\pi = (m_1, m_2, m_3)$一并发给验证方。

当验证方收到证明$\pi$之后，他只需要根据这几个数字和哈希函数$H$重新生成$rand_1, rand_2$，就可以验证证明是否准确了。

CRS模型

公共参考字串（CRS）是一个非常简单的假设，具体是这样的：

我们假设在一个协议中，证明方与验证方都拥有一段相同的参考字串。这个字串可能是随机生成的，也可能是某个函数的输出。重要的是完成协议的两方并不知道这个字串具体是如何被生成的，就感觉像是天上掉下来的一样。

通过CRS，我们可以粗略构建CRS模型下无交互LPCP的大概步骤：

  1. 首先，第三方根据LPCP用到的R1CS电路，选取随机数$r$，并且根据随机数生成好Query部分，即$q_1,q_2,q_3$，然后丢入CRS当中。
  2. 证明方准备好自己的证明向量$\pi = [w, h(m+1), …, h(2m-1)]$，然后从CRS中取出Query向量的右半部分，即$q_1^R, q_2^R, q_3^R$。随后分别和自己的证明向量相乘，得到我们要的$a,b,c$三个值。

$$ a = \langle [q_1^R 0^{m-1}], \pi \rangle\\ b = \langle [q_2^R 0^{m-1}], \pi \rangle\\ c = \langle q_3^R, \pi \rangle $$

  1. 证明方把$a,b,c$发送给验证方。
  2. 验证方根据CRS得到$q_1^L, q_2^L, q_3^L$，然后结合证明方提供的a,b,ca,b,c，检查等式是否相等:

$$ (\langle q_1^L, [1, x] \rangle + a) \cdot (\langle q_2^L, [1, x] \rangle + b) \stackrel{?}{=} (\langle q_3^L, [1, x] \rangle + c) $$

  1. 如果相等，即代表LPCP验证通过。

通过CRS假设，我们可以通过。但是，直接共享明文的字串会让证明者可以预知自己的挑战，进而根据挑战作弊。同时，在裸露的LPCP体系下，证明方需要将完整的证明$\pi$传给验证者，违背了“零知识”的前提。

因此，无论是初始的CRS，还是后续的整体运算都需要在加密空间下进行，而且这层加密应当是不可解的。特别的是，这里的加密方式需要保证，加密后的字串$[[a]]$具有与原字串$a$具有相同的（至少具备LPCP所需的）运算性质。这样，这层加密可以无缝地融入原有的LPCP体系，验证方无需解密即可直接检验证明。

零知识

线性加密系统Linear-only Encoding

首先，为了防止证明方实现看到Query的内容进行作弊，我们的加密系统一定要能够隐藏Query本身。也就是说看到密文的证明方并不可以得到任何和原文有关的信息。这一点所有的加密算法都可以做到。

其次，我们需要保证证明方仍然可以生成内积$[[\langle q_i, \pi \rangle]]$，并且最后验证方可以进行验证。这一点其实是一个非常独特的需求，我们可以把这两个要求拆开来看一下：

  1. 证明方可以生成内积$[[\langle q_i, \pi \rangle]]$。因为$\pi$里面也就是一串数字，所以这就是说证明方可以输出Query中$[[q_i]]$的数值与$\pi$向量的数值的线性组合。完成这一点我们可以使用拥有加法同态特性的加密算法。
  2. 验证方可以验证$[[a]] \cdot [[b]] = [[c]]$。这也就是说，证明方通过加法同态性质得到的加密过后的$[[a]], [[b]], [[c]]$需要通过类似于乘法同态一样的验证。这一点要求比较特殊，我们在选择加密算法的时候要额外注意。

初次之外，为了安全性，一个线性加密系统还需要满足两条额外的属性（properties）：

单向性（One-way）：这条属性是说，如果看到了$[[x]]$，我们不能推导出$x$的值。这一点确保了密文是安全的。

仅限线性组合（Linear-only）：这一点要求了，如果给定了一组密文$[[x]],[[y]]$，我们只能生成这组密文的线性组合，即$[[ax+by]]$，但是不能生成任何其他的值来。这一点确保了我们不能在没有密钥的情况下任意生成合理的密文。

一般来说，满足这些要求的线性加密系统很少。一个最常见的例子，就是有Pairing配对属性的循环群$G$了，比如说某些椭圆曲线。

在循环群中，我们拥有生成元$g \in \mathbb{G}$。加密一个数字$x$就是$g^x$，然后任何人都可以获得$g^x$的线性组合（即$(g^x)^a g^y = g^{ax + y}$），但因为离散对数的困难性，很难通过$g^x$推导出$x$。

同时，因为我们选择的循环群拥有配对操作，所以我们可以非常轻松的验证密文的乘积是否相等。 $$ x_1 \cdot x_2 \stackrel{?}{=} \alpha \cdot x_3\\ e(g^{x_1}, g^{x_2}) = g^{x_1 x_2}_T \stackrel{?}{=} g^{\alpha x_3}_T = e(g, (g^c)^\alpha) $$ 有了线性加密系统之后，我们之前在尝试无交互LPCP的时候遇到的作弊问题就引刃而解了。

随机线性检查（Random Linearity Check）

当我们加上了线性加密系统之后，现在得到的SNARK还有一个巨大的漏洞。

我们观察发现，因为Query的部分都是加密隐藏起来的，所以证明方还可以做一个骚操作：在$[[a]],[[b]],[[c]]$的时候，在中途偷偷的变换用到的证明$π′$。因为证明方也可以自己跑$QuadTest$算法，他可以使用三个不同的$π′$值来得到最后的密文，并且使得密文的乘积相等，可以通过$QuadTest$测试，并且欺骗验证方。

这一问题解决的方法也不难，我们需要修改一下LPCP协议，在中间多加上一个随机线性检查（Random Linearity Check）。

在我们生成LPCP的Query$q_1^R, q_2^R, q_3^R$的时候，我们随机的选取$\alpha, \beta, \gamma$，然后额外的生成一个线性检查Query $q^* = \alpha q_1^R + \beta q_2^R + \gamma q_3^R$。我们把$q^∗$也发送给证明方，并且要求证明方提供$⟨q^∗,π⟩$的内积$d$。

这样一来，最后验证方可以收到四个数字，即$a,b,c,d$。这个时候验证方就可以验证： $$ d \stackrel{?}{=} \alpha a + \beta b + \gamma c $$ 如果符合检查的话，那就表示证明方在生成$a,b,c,d$的时候，用到的是同样的$\pi$了。

同理可得，在SNARK中，我们需要在$Setup$阶段额外的生成一组$q^∗$。随后我们在在$S_v$中额外添加$[[q^{*L}]], [[\alpha]], [[\beta]], [[\gamma]]$，并且在$S_p$中添加$[[q^{*R}]]$。随后，证明方提交的证明中额外需要提交一个$[[d]] = \langle q^{*R}, \pi' \rangle$。

这样一来，验证方可以首先通过$QuadTest$，验证$[[a]],[[b]],[[c]]$与$[[d]]$之间的关系，确保证明方没有做弊。验证通过之后，再验证$[[a]],[[b]]$与$[[c]]$的关系。如果两次检查都通过了，那就基本上等于LPCP通过了。

加上随机线性检查之后，我们就得到了zkSNARK中的SNARK的完全体了。

初始化

其实，这里还有最后一个漏洞——初始化方可以掌握先行加密系统的公钥和私钥，这样CRS就再一次变为了明文的区域。对于这个问题可以考虑多方加密，一层套一层，保证任何人都无法掌握整个$S(C)$。

ETH智能合约

工具链

Solidity

用于编写ETH智能合约的DSL

Remix

编写ETH智能合约的一个在线IDE，可以使用本地JS VM/测试链调试合约

MetaMask

Chrome钱包插件

Zokrates

编写zk-SNARK的DSL，可以编译生成Solidity代码

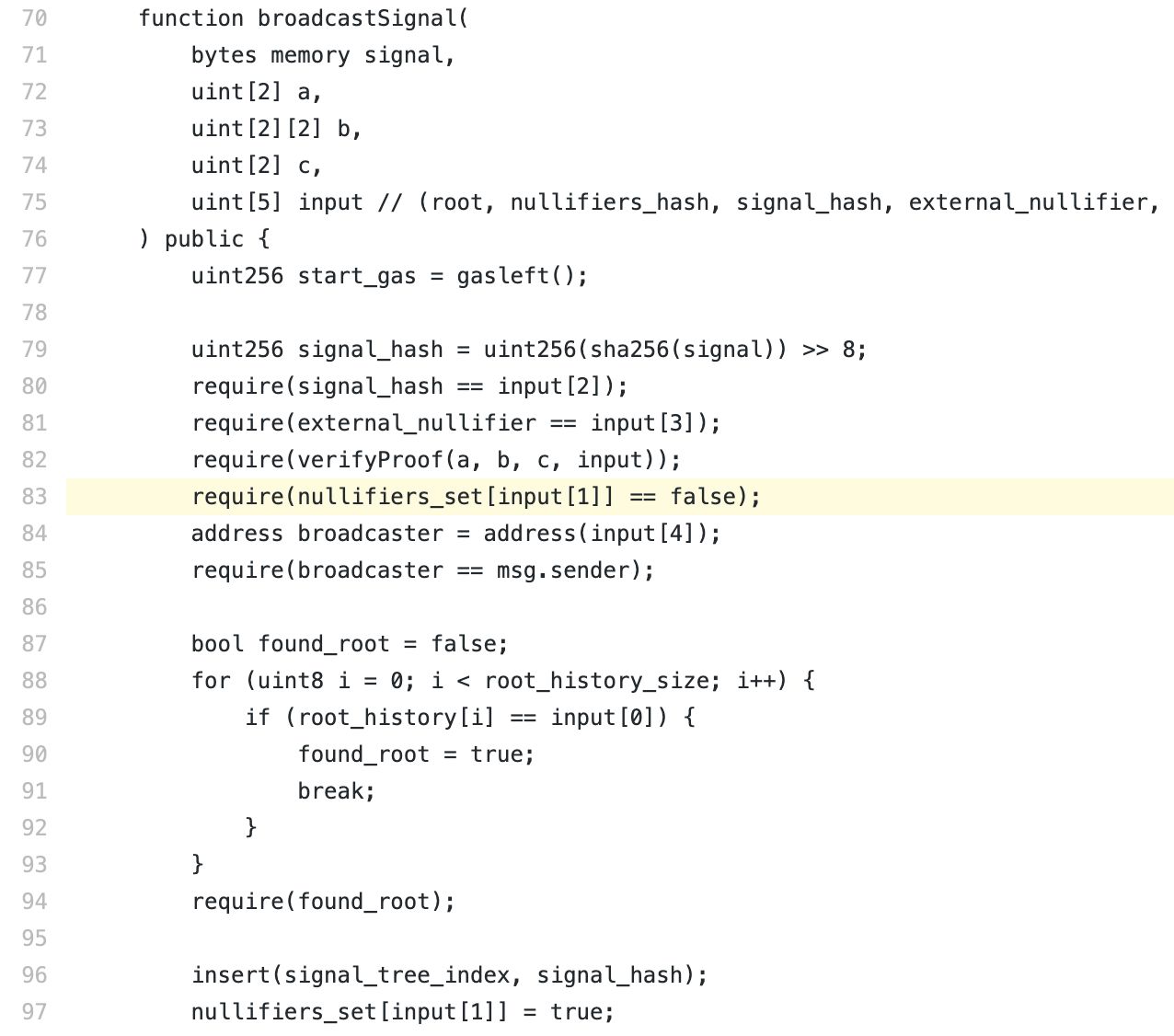
安全问题

输入假名

参见：输入假名

semaphore.jpg
semaphore.jpg

成因很简单——选取的模数域小于Solidity的整数范围，同时又没有检验输入的大小，因而导致多个不同的输入取模后相等，导致双花攻击。